GRAPHS ON THE GO: GRAPHS ON THE GO: Understanding polynomials - (Concavity)

A very important concept to understand graphs and their nature which leads to better graph plotting.

Now its time to understand what is concavity-

Concavity helps us define the shape of graph in a better way and make it more precise-

Lets take an example in which we found out that a graph in increasing, now what kind of shape it will take up-

There are two possible cases-

Now if we observe in both shapes the graph is increasing but now question is how to know which one to of them should be the shape of requisite graph?

Here come concavity which helps you know if the graph is of CASE 1 or CASE 2.

CASE 1: It is concave up.

CASE 2: It is concave down.

Now how can we find the concavity of the curve-

Concavity is determined by finding the rate of change of slope of the function.

which means-

It is the second derivative of the function as slope is the first derivative of the function.

Now if in that particular region-

CASE 1: Second derivative > 0   - Concave up

CASE 2: Second derivative < 0   - Concave down

CASE 3: Second derivative = 0   - Point of inflection.

Till now we are clear what is concave up or concave down but what is this point of inflection?

Point of inflection is a point where the change in slope is zero.

For example in -

y = x³

at x=0 there exists a point of inflection.

Now taking the example of y = x³ we will understand all three cases-

The first derivative comes out to be 3x² which is always positive implies that the graph is increasing for all real values x.

Now finding the second derivative which comes out to be 6x which has 3 cases-

CASE 1: x > 0 , here the second derivative is positive.       - Concave up 

CASE 2: x < 0 , here the second derivative is negative.      - Concave down

CASE 3: x = 0, here the second derivative is zero.              - Point of inflection

Also the it has only one real root which is at x = 0.

Now we have all the things required to plot its graph-

A summary to that is -

root at x = 0.

increasing for all real x.

x > 0 -concave up , x < 0 -concave down , x = 0 Point of inflection.

Now let's see hope the graph looks like-

It is same as we predicted using our method.

Notice carefully the following animations under the questions in order to get a clear idea.

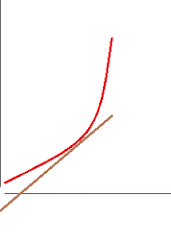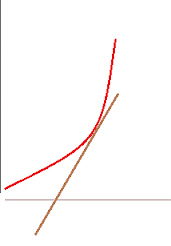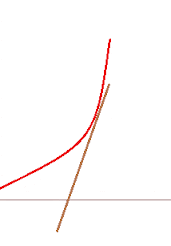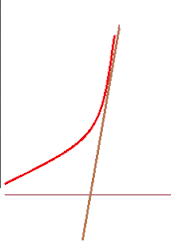
Visualising why an increase in slope of the the function gives out concave up?

This animation shows clearly why the we get concave up when the slope is increasing or when the second derivative is positive.

Visualising why an decrease in slope of the the function gives out concave down?

As we already know that the slope at any point is the angle made with positive x axis, and from the above animation it is quite clear that in this case the angle with positive x axis is decreasing and hence the second derivative is also negative and hence concavity down is also explained clearly.

Visualising why no change in slope of the the function gives out a point of inflection?

For this i will request you to see the y = x³  again and see that the slope near 0 is always same and hence gives change in slope equal to zero, hence second derivative is zero and which implies the slope neither increases nor decreases at that point, hence x = 0 is the point of inflection for y = x³.

Hope the concept of concavity is clear.

(Image credits- https://www.desmos.com/)

Stay Tuned for the next post.

For any query comment down there.

#graphs_on_the_go  #understanding_graphs #mathematics, #feed-o-math , #quadratic_equations , #polynomials , #graphing_polynomials